在平面幾何中,有一條著名的定理:在直角三角形中,兩直角邊的平方和等于斜邊的平方,也就是C2=A2+B2。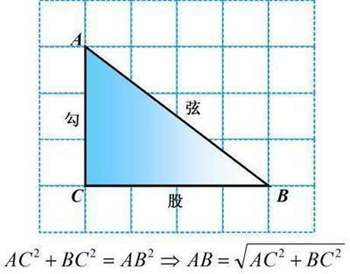 在西方人的眼里,這條定理是由畢達(dá)哥拉斯在公元前500年的時(shí)候發(fā)現(xiàn)的,因此,他們把這稱為畢達(dá)哥拉斯定理。其實(shí)在我國(guó)現(xiàn)存最早的數(shù)學(xué)著作《周髀算經(jīng)》上,就已經(jīng)記載了公元前六七世紀(jì)榮方和陳子有關(guān)這條定理的一段對(duì)話,陳子說(shuō)“若求邪(斜)……勾股各自乘,并而開(kāi)方除之”。這段話用公式表示即為:c等于根號(hào)下a平方加上b平方或c平方等于a平方加上b平方。因?yàn)殛愖邮潜犬呥_(dá)哥拉斯早,因此有人主張把“畢達(dá)哥拉斯定理”改稱“陳子定理”。1951年,我國(guó)的《中國(guó)數(shù)學(xué)》雜志以“勾股定理”為其命名。 勾股定理是幾何學(xué)中一顆耀眼奪目的明珠,被稱為“幾何學(xué)的基石”,而且在高等數(shù)學(xué)和其他學(xué)科中也有著極為廣泛的應(yīng)用。 |
熱門搜索:十萬(wàn)個(gè)為什么 為什么井蓋是圓的


